Tuesday 3 April 2012

1.6 COULOMB'S LAW



Any two charged objects will create a force on each other.   Opposite charges will produce an attractive force while similar charges will produce a repulsive force.  The greater the charges, the greater the force.  The greater the distance between them, the smaller the force.  For two spherically shaped charges the formula would look like:
charges.gif (1236 bytes)
  • F  the force on each charge, + indicates repulsion, - indicates attraction
  • k the electrostatic constant  
  • q1 the quantity of charge 1 measured in coulombs
  • q2 the quantity of charge 2 measured in coulombs
  • r the radius of separation from center of one charge to the center of the other.
The forces are force pairs of each other so they will always be equal in size and opposite in direction. 


COULOMB'S LAW IN VECTOR FORMSuppose that two charges, $q_1$ and $q_2$, are located at position vectors ${\bf r}_1$ and ${\bf r}_2$. The electrical force acting on the second charge is written 
\begin{displaymath} {\bf f}_2 = \frac{q_1 q_2}{4\pi \epsilon_0} \frac{{\bf r}_2 - {\bf r}_1} {\vert{\bf r}_2-{\bf r}_1\vert^{3}} \end{displaymath}
\begin{figure} \epsfysize =2in \centerline{\epsffile{fig24.eps}} \end{figure}



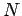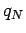Consider $N$ charges, $q_1$ though $q_N$, which are located at position vectors 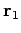${\bf r}_1$ through 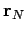${\bf r}_N$. Electrical forces obey what is known as the principle of superposition. The electrical force acting on a test charge 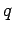$q$ at position vector 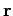${\bf r}$ is simply the vector sum of all of the Coulomb law forces from each of the 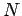$N$ charges taken in isolation. In other words, the electrical force exerted by the 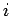$i$th charge (say) on the test charge is the same as if all the other charges were not there. Thus, the force acting on the test charge is given by 
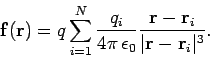\begin{displaymath} {\bf f}({\bf r}) = q \sum_{i=1}^N \frac{q_i}{4\pi \epsilon_0} \frac{{\bf r}-{\bf r}_i}{\vert{\bf r}-{\bf r}_i\vert^3}. \end{displaymath}


Example 4 Coulomb’s law for electrostatic force between two point charges and Newton’s law for gravitational force between two stationary point masses, both have inverse-square dependence on
the distance between the charges/masses. (a) Compare the strength of these forces by determining the ratio of their magnitudes (i) for an electron and a proton and (ii) for two protons. (b) Estimate the accelerations of electron and proton due to the electrical force of their mutual attraction .

ANS= USE F[e]/F[g]





Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)